
|
1.2.1 Requirements for the Star Trek cartography
| Before we can start to deal with the actual Star cartography and to put together its building blocks, which are provided by the episodes, movies and official books, to a logical and coherent picture of the Star Trek universe, we still have to clarify a) how these building blocks look like and b) how we can use them to reach our goal. Therefore, in this chapter, the tools necessary for the real stellar astronomy as well as the fictional Star Trek cartography shall be fixed. |
|
The cartography as a
scientific field which is in the real world very important, too, mainly requires
knowledge in mathematics, especially trigonometry and spatial geometry, and in the
analysis, interpretation and graphical representation of huge amounts of data. These
points are the basic requirements for the Star Trek cartography as well, although this
"new" field of course has special demands.
At any rate, the application of fundamental scientific methods is the basis for all other
work. Nowadays, they can often be carried out very easily with the computer, but the
use of rudimentary tools is possible as well. For example, Rick Sternbach, senior
illustrator and technical consultant of Star Trek: Voyager, does not need a
sophisticated spreadsheet / 3D vector drawing program to calculate the course of Voyager,
but marks the points of interest on usual 11'x17' paper. Sometimes, it is indeed
useful (especially with maps) to illustrate things directly on a sheet of paper, however, in this
project as often as possible the most accurate methods shall be applied, i.e. mathematical
calculations and electronic picture and data processing.
Another requirements is, of course, the exact knowledge of the data to be processed. In
the case of the Star Trek cartography, this is the knowledge of all Star Trek episodes,
movies and books. However, this is only a part of the special demands of the Star Trek
cartography. Indeed, the real astronomy is of considerable importance; in the end, this
projects mostly deals with astronomy, and even if the data basis is fictitious, cartographic
and astronomical procedures are used for its evaluation. Beside special material
(celestial maps, astronomical data tables etc.), this also includes three-dimensional
spatial geometry and astronomical calculations. A complete list of the used material you
can find in the sources.
But also the project itself contains several tables and data collections especially
created for the Star Trek cartography which could prove useful for the further work. They
are available in the section "Resources", while special algorithms of the Star
Trek cartography you can find in "Interactive programs".
After this general overview over the necessary means and methods, now the most important
aspects of the Star Trek cartography shall be examined more profoundly.
1.2.2 Distances as basis for the cartography
Because Star Trek usually does not provide us with complete maps, but at most with maps showing a mission-specific, small part of space instead of the whole explored space, we usually have to fall back on the smallest building blocks of the Star Trek cartography, with which we still have to build a complete picture of the universe: the distances given in episodes, movies and books. As soon as we have a large enough number of distances which are reciprocally associated with each other (that means for every location, the distance to every other location must be known), we can create a map based on this distances. However, the issue isn't that easy because unfortunately, we never have a complete collection of distances and our knowledge is always sketchy because of the minor significance of cartography in Star Trek. With such an open web of figures unambiguous maps are impossible at any rate, therefore we must rely on assumptions, speculations and logical premises, the second-most important corner stone of the Star Trek cartography, and have to accept that there will never be a unambiguous, not interpretable picture of the Star Trek universe, even if e.g. an official technical manual "officialises" one of the infinite possibilities some day.
The application of distances as basis for the cartographic work is even more difficult because of the fact that the sources usually do not provide us with direct figures. In fact, there are 4 different ways to determine distances from official sources (episodes, movies, books, electronic media), which are introduced in the next paragraphs.
 |
A nearly complete collection of all distances directly given in the series, movies and books or determined by the shown methods you can find in the resource Star Trek distances. |
1. Directly given distances
In general, the episodes and movies are very thrifty in the use of distances in dialogues, on computer displays etc.; only Star Trek: Voyager includes direct distances to object situated near the route of the USS Voyager more often. Nonetheless, there are figures for nearly all distances between the important planets (i.e. the core planets of alliances and empires) thanks to some key episodes, but also official documentation like the ST:DS9 Technical Manual. Distances listed in such books or mentioned in dialogues are usually given in the popular scientific unit light year (ly), in some cases, however, also the astronomical unit (AU) and the parsec (pc) were used. Although the direct application of distances is the fastest and most comfortable way to get information on star positions and distances, also in these cases a mathematical conversion is sometimes necessary because naturally all distances must be available in the same, standardized unit for the evaluation and visualization in maps (in the real-life astronomy, the parsec, on Star Trek and therefore in this project the light year).
| Unit | Definition | Conversion |
| Light year (ly) | Distance which light in a vacuum travels in one year (V=299792 km/s). | 1 ly = 9.461x1012
km 1 ly = 6.323x104 AE 1 ly = 0.307 pc |
| Parsec (pc) | The distance, from which one astronomical unit becomes visible under an angle of one arc second. | 1 pc = 3.086x1013
km 1 pc = 2.063x105 AE 1 pc = 3.262 ly |
| Astronomical Unit (AU) | Mean distance of Earth from the Sun. | 1 AU = 149.6x106 km 1 AU = 1.582x10-5 ly 1 AU = 4.847x10-6 pc |
2. Determine distances by time and velocity
Mainly in Star Trek:
The Next Generation, but partly also in the other series and the movies one can find an
important indirect type of distance figures, which is closely associated with the
interstellar voyages with a starship: the specification of warp factor and time. A typical
example is that we know the current position of a starship like the USS Enterprise-D and
we get to know in the dialogue, in the The Next Generation preferably with Lt.
Cmdr. Data,
the necessary warp speed at which the ship reaches a goal in a certain amount of time.
Therefore, absolute requirement for this method is the knowledge of starting point and
destination beside the time and velocity because otherwise, the figures are useless.
If all values are given, the determination of the distance is quite simple, since we only
have to apply the mathematical standard formulae (s=v*t) to calculate the distance.
However, it has to be taken into consideration that on Star Trek, velocities are never
given in km/s, but in warp factors or impulse fractions and therefore their is the problem
to convert these special velocities into SI units. Fortunately, the ST:TNG Technical
Manual and Star Trek Encyclopedia include tables of the multiples of the light speed (c)
or the km/s certain warp factor or impulse fractions correspond to. Hence, in most cases
the calculation should not be a problem.
| Velocity | v/c | km/s |
| 1/4 impulse | 0.0625 | 18737 |
| 1/2 impulse | 0.125 | 37474 |
| Full impulse | 0.25 | 74948 |
| Warp 1 | 1 | 299792 |
| Warp 2 | 10 | 2997920 |
| Warp 3 | 39 | 11691888 |
| Warp 4 | 102 | 11691888 |
| Warp 5 | 214 | 30578784 |
| Warp 6 | 392 | 64155488 |
| Warp 7 | 656 | 117518464 |
| Warp 8 | 1024 | 306987008 |
| Warp 9 | 1516 | 454484672 |
| Warp 9.2 | 1649 | 494357008 |
| Warp 9.6 | 1909 | 572302928 |
| Warp 9.9 | 3053 | 915264976 |
| Warp 9.99 | 7912 | 2371954304 |
| Warp 9.9999 (Subspace radio) | 199516 | 59813300672 |
Unfortunately, sometimes it isn't that easy simply to search the corresponding km/s value
from a table. In some cases that distances isn't given directly, but is described by
phrases like "at high warp" or "at maximum warp". Concerning
indefinite expressions, it is usually only possible to use a velocity range and therefore
to calculate only a distance range (minimum and maximum distance), however, there is a
possibility for a direct determination if "maximum warp" is mentioned. We know
the speed limit of quite a lot starship classes, although we have to differentiate between
highest sustainable speed (without time limit) and maximum speed (only for a fixed time;
usually 12h), depending on the given time. Another problem is that newer classes like the
Defiant, Sovereign and Intrepid class have maximum speeds not mentioned in any official
table. In these cases we can only use semi-official approximate values which are listed in
the following table.
| Class | Highest sustainable speed | Maximum speed (12h) |
| Miranda class | Warp 9.2 | |
| Nebula class | Warp 9.6 | |
| Galaxy class | Warp 9.2 | Warp 9.6 |
| Akira class | Warp 9.8 | |
| Defiant class | Warp 9 | Warp 9.982 |
| Intrepid class | Warp 9.975 | |
| Sovereign class | Warp 9.95 |
| Velocity | v/c | km/s |
| Warp 9.8 | ~2500 | 749480000 |
| Warp 9.95 | ~5500 | 1648856000 |
| Warp 9.975 | ~6667 | 1998713264 |
| Warp 9.982 | ~7500 | 2248440000 |
However, the conversion becomes more difficult if a fractional warp factor is given which
isn't listed in any of the above tables. Then, we have to use a conversion formula from
warp to c. Unfortunately, none of the official documentations mentions such a formula. The
only clue is the exact graph of the so-called warp function depicted in the ST:TNG
Technical Manual, which approaches an infinite value if the warp factor approaches 10
(asymptotic graph). Numerous popular formulae developed by fans are based on this graph,
but none of them can reproduce the exact curve. This is only possible until warp 9,
because until this value, the function has a quite simple graph:
f(x)=x(10/3)
Only between warp 9 and 10 the asymptotic gradient has an effect on the graph, so that a correction factor has to be added. A possible formula for that is
f(x)=x
(10/3)+(10-x)(-11/3)which, however, does only produce the exact factors of the light speed listed in the table until warp 9.6.
 |
Use the interactive program Warp-time-distance for the automatic calculation of distances on the basis of a time and whole or fractional warp factors until warp 9.6. |
3. Distances of real stars
Of course, it is
rather improbable that a destination whose distance has to be determined is a
"real" star, however, it has quite often been the case, especially in the
original Star Trek series. On the whole, 34 stars have been mentioned in Star Trek in the
dialogue or were part of the action as shown locations.
If we actually have a real star, we then only have to look up this star in a stellar
atlas, and hopefully we will find a distance figure. However, a partly uncertainty remains
because unfortunately, due to different or inaccurate determination methods there is a
controversy about the exact distance of some stars.
| Especially the most often used method, the determination of distances by the star parallax (the angle under which one would see the distance Earth-Sun from the star) becomes more and more inaccurate with increasing distance of the star, until the error deviation exceeds the actual distance and the measured value is therefore useless. The big problem concerning this issue is, that the parallax determination using conventional, earth-bounded telescopes produces large error deviations already with low distances, because these devices can only measure angles accurately up to some thousand arc seconds ("). Therefore, the deviation with 30 ly is 7%, with 150 ly already 35% and with 350 ly even 70%. | 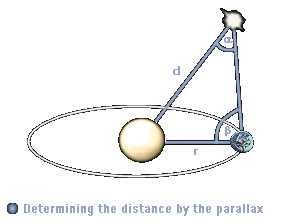 |
Exclusively because of the HIPPARCOS mission we have nonetheless relatively accurate distances for all 34 stars. During this mission, which lasted from 1989 to 1983, a satellite measured outside Earth's atmosphere and its interferences the distances to the most important stars with an unequalled precision. Since 1997, the HIPPARCOS catalogue is available, from which the distances of all real stars listed in this project were taken.
 |
An overview of the real stars mentioned in Star Trek, their parallaxes and distances you can find in the table The positions of the real stars. |
4. Measuring distances in maps
It happens relatively
seldom that in Star Trek maps of certain galactic regions are shown on screen, and almost
never a map of the entire Galaxy is displayed. Often the problem arises that the maps,
which are mostly displayed on computer screens, are much too small, indistinct and blurred
so that they are virtually useless. Nevertheless, there is a considerable number of known
maps from Star Trek: Voyager, Star Trek: Deep Space Nine and official manuals like the
ST:DS9 TM, which we can use for the cartographic analysis. The actual measuring of
distances is relatively easy, however, there are some restrictions and problems which have
to be considered first.
Basically, we can only measure distances if we know the pixel-light year-ratio (px/ly ratio) of the map. This value we can derive from
the map scale. With this requirement, most of the available maps have to be ruled out,
because only few of them show a scale. Until now, this is only the case with the maps of
the ST:DS9 TM. Here, we have a measuring bar on the map, with which we can calculate the
searched distance quite easily. Using a ruler and a calculator is surely the quickest way,
however, for really 100% accurate results the demanded map should be scanned without any
distortions. Subsequently, the single distances should be measured in an image editor. The
easiest way is to use a program which can display the length of lines of any angles;
unfortunately, most programs do not have this useful function. Therefore, you additionally
need a calculator to calculate the distances with right-angled triangles, as shown in the
following simple example:
| 1. First, the px/ly
ratio has to be determined. For this, determine the length of the measuring bar and
calculate the ratio: Ratio=Light years / Length = 10 ly / 49 px = 0.204 ly/px 2. Measure either the length of the connecting line between the starting point and the destination directly (if possible) or construct a right-angled triangle, whose adjacent leg length and counter opposite leg length you measure and subsequently calculate the length of the hypotenuse by the Pythagoras theorem. Pixel length=sqrt(a�+b�)=sqrt((147 px)� * (18 px))�=148.1 px 3. Multiply the pixel length by the px/ly ratio of the map to get the searched distance. Distance=148.1 px * 0.204 ly/px = 32.22 ly |
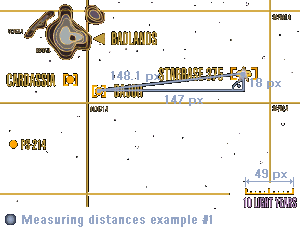 |
If there isn't any scale figure on the map, there is sometimes nonetheless a possibility
to get the px/ly ratio, namely in those cases, when the map includes distances whose
length is already known. The ratio can then be determined by measuring the line length or
constructing a right-angled triangle and using the Pythagoras theorem. Afterwards, the
px/ly ratio can be used to convert the pixel length into the searched distances, how it
was shown in the above calculation and it is shown in the following second example.
| 1. The map on the
right does not contain any scale, however, the diameter of the Romulan Neutral Zone is
known from Star Trek: The Next Generation: 1 ly. With the Pythagoras theorem, we got a
pixel length of 25.5 px for this diameter, so that we can calculate the ratio: Ratio=Light years / Length = 1 ly / 25.5 px = 0.039 ly/px 2. This time, the distance of Romulus from the Neutral Zone shall be determined. In this connection it has to be taken into consideration that the distance point-straight line always refers to the perpendicular through the point on the straight line (i.e. that the intersecting angle between the connecting line and the border line of the RNZ must be a right angle). Only then the distance is really the shortest one. Because we have an oblique line again, we have to use the Pythagoras theorem to get the distance: Pixel length=sqrt(a�+b�)=sqrt((76 px)� * (28 px))�=81 px 3. Finally, multiply the pixel length by the px/ly ratio of the map to calculate the distance of Romulus from the Neutral Zone. Distance=81 px * 0.039 ly/px = 3.18 ly |
|
A last piece of advice concerning the derivation of distances from maps: maps of the
real Galaxy are only limitedly useful for the measurement, because they are a
two-dimensional reproduction of the real positions of the stars in the three-dimensional
space. Hence, the shown distances are always only the minimum distance to Earth, and it is
very probable that the considered star is much farther away because most of them are not
located in the same plane as Earth. Three-dimensional maps, on the other hand, can't be
used at all for the determination of distances without considerable calculation efforts.
 |
Numerous maps from both real astronomy books and Star Trek episodes and documentations, which you can derive distances from, you can find in the maps archive. |
1.2.3 The purpose of real stars for the cartography
Beside the already
given positions of stars and planets in official maps it is possible to derive further
fixed points from the episodes, movies and official documentation by regarding the 34 real
stars. We have already used these special locations in the last paragraph to determine
their distances to Earth, in order to use the various coherent distances to get to know
their spatial situation.
Now, we will take a step forward and calculate the real position of those stars in the
three-dimensional space. Of course, this is associated with considerable efforts. However,
these efforts will take us much closer to our goal of a Galactic map that is realistic,
detailed and coincidentally confirmed by most of the episodes, because we know
enough real stars to use them as a "basic framework" for all fictitious components
of the map.
To determine the real,
absolute positions of the stars in the Galaxy it is inevitably necessary to deal with the galactic coordinate system very intensively, which is a very powerful,
but rather neglected astronomical system.
With the increasing exploration of our Galaxy and its structure, the galactic coordinate
system has been developed by the astronomers because of their desire to learn more about
the concentration and distribution of the stars in the Milky Way. It is considerably
ponderous to use the conventional coordinate systems (like the equatorial system) for this
special field of the astronomy called stellar statistics, because for the determination of
the real situation of the stars in space, and not at the sky, you always need the distance
of the star beside its right ascension and the declination. On the other hand, with
galactic coordinates, which refer to the Milky Way, additional distance figures are not
needed.
The reason for this peculiarity is that the galactic coordinate system is the sole system
which is not based on earth-bounded (and partly distance or time dependant)
celestial coordinates, but which uses points of superior systems as definition
parameters. The reference plane or basic circle of this coordinate system is the Galactic plane (the symmetrical plane of our Galaxy), the Galactic center is used as reference point. Simultaneously,
the Galactic core is the longitudinal zero-point, that means the direction towards the
Galactic center has a galactic length of 0�. The galactic longitude l is the counterpart to the right ascension
(the azimuthal / longitudinal angle) and increases in the same direction
(counter-clockwise) in a degree-based system from 0� to 360�. The second necessary
coordinate is the counterpart to the declination (the elevation angle), the galactic latitude b, which decreases from the Galactic north pole with b=90� and the Galactic plane with
b=0� to the Galactic south pole with b=-90�.
To calculate both galactic coordinates from the equatorial coordinates, at least the
coordinates of two fixed points are needed: the Galactic center and the Galactic north
pole. Both values are currently only available for the equinox (the astronomical epoch)
1950.00. The Galactic center has the right ascension 17h42.4min
and the declination -28�.92, and the Galactic north pole has the right ascension 12h49min
and the declination +27�.4.
The following example, Vulcan (=o2 Eridani or 40 Eridani), shows how galactic
coordinates can be calculated:
1. We look up the equatorial coordinates of the star. Vulcan has the right ascension 04h13min and the declination -7�.44'.
2. The right ascension has to be converted from time-based coordinates (hour h, time minutes min and time seconds s) into degree-based coordinates (Degrees �, Arc minutes ' and Arc seconds ''), which are used for both the declination and the galactic coordinates. For this purpose, we first divide the time seconds (if given) by 60 and add the hours in order to get a right ascension only in hours (as a decimal number). For Vulcan, this leads to (13/60)+04=4.h21667. To convert the time-based angle into a degree-based angle, the result has to be multiplied by 15 (1h=15�): 4.h21667*15=63�.25.
3. For the actual conversion into galactic coordinates, some formulae of the spherical trigonometry are needed. The galactic latitude b we calculate from the right ascension a and the declination d with
sin b=sin d * cos 62�.6 - cos d * sin 62�.6 * sin(a-282�.25)
For Vulcan, this results in sin b=-0.6136 and therefore b=-37�.85.
For the somewhat more difficult calculation of the galactic longitude l, we need the calculated galactic latitude:
cos(l-33�) = ( cos d * cos(a - 282�.25) ) / (cos b)
For Vulcan, we get sin
l-33�=-0.9759 and therefore l-33�=167.4� and finally l=200.4�.
With these formulae given in specialist literature, the problem arises that they oddly not always produce the right values. The galactic latitude is always correct, however, the galactic longitude deviates with half the values by 0� till 200�. Of course, this is unacceptable, so that a second method for the determination of galactic coordinates becomes necessary, in order to get comparison figures for the calculated values.
What can we now do
with these galactic coordinates? If you take a look at the fixed points of the galactic
coordinate system - north pole, south pole, Galactic plane, it becomes clear that in this
system, the stars are quasi projected on a Galactic sphere,
whose equator is the Galactic plane. We can now put Earth in the center of the Galactic
sphere, because she is located very near to the Galactic plane and we have fixed all
definition parameters (Galactic north pole, zero-point) by our earth-based equatorial
system.
If we draw the fixed points, Earth and a star whose position is searched in a model of the
galactic coordinate system, we see that the position of this star relative to Earth can
be determined with simple trigonometric calculations.
| For this purpose, we
firstly need the azimuthal and elevation angels, which we already have as galactic
coordinates, and the distance of the star from Earth on the galactic plane (the
"two-dimensional" distance). The latter value we can calculate from the real
distance of the star (which is the hypotenuse of a right-angled triangle) by angle
relations: dplane=cos(b) * d With the plane distance and the two angles we can now easily determine the x, y and z distances of the star from Earth by calculating the length of the line with the starting point (0,0,0) (that is Earth), the length dplane and the angles l and b:
Yrelative=.-cos(lplane) * dplane barc=b*(pi/180�) |
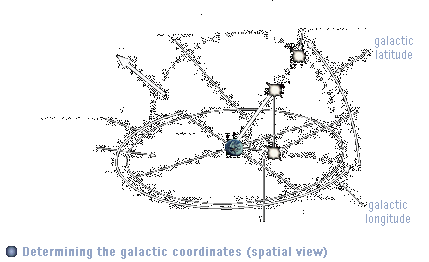
|
If we look at the Galactic plane "from the top", rotated in that way, that 0� galactic longitude are the exact vertical intersection line of the Galactic equator, then all stars with a positive relative x coordinate are located right from Earth on the plane, with positive relative y coordinate below Earth on the plane, and with positive z coordinate (spatially) above Earth and the Galactic plane. Hence, the star in the above example has positive x,y and z coordinates.
With repeating the described procedure for a sufficiently large number of stars and transforming the relative coordinates according to a fixed pixel-light year-ratio, galactic maps can be created very easily.
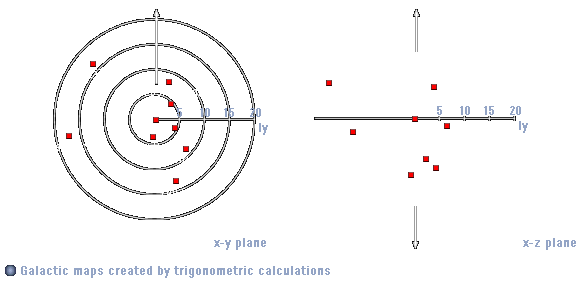
 |
A complete collection of all real stars mentioned in Star Trek and their distances, galactic coordinates and calculated absolute coordinates in several systems you can find in the table The positions of the real stars. |
Now that you have learned the basic knowledge of the Star Trek cartography and know how to apply the different tools and methods, the actual journey through the Star Trek Galaxy is about to commence.
� 1999-2001 by Star Trek Dimension / Webmaster. Last update: April 25th, 2000