
|
1.2.1 Voraussetzungen der Star Trek Kartographie
| Bevor wir beginnen können, uns der eigentlichen Star Trek Kartographie zu widmen und all die Bausteine, die uns in den Episoden und offiziellen Büchern gegeben werden, zu einem logischen Bild des Star Trek Universums zusammenzusetzen, gilt es noch zu klären, a) wie diese Bausteine aussehen und b) auf welche Weise wir diese zum Erreichen unseres Ziel verwenden können. In diesem Kapitel soll deshalb das "Handwerkszeug" festlegt werden, daß für die Kartographie im allgemeinen und die Star Trek Kartographie im speziellen notwendig ist. |
|
Die Kartographie als
ein wissenschaftliches Fachgebiet, daß auch in unserem heutigen Leben schon eine große
Rolle spielt, setzt dabei vor allem Kenntnisse in der Mathematik, besonders der
Trigonometrie und Raumgeometrie, und in der Auswertung, Interpretation und Darstellung von
großen Datenmengen voraus. Diese Grundvoraussetzungen gelten genauso auch für die Star
Trek Kartographie, obwohl dieses "neue" Fachgebiet natürlich noch spezielle
Anforderungen stellt.
Die Anwendung grundsätzlicher wissenschaftlicher Methoden stellt aber auf jeden Fall die
Basis für alle weitere Arbeit dar. In der heutigen Zeit können diese häufig
automatisiert und sehr einfach mit dem Computer erledigt werden, aber auch die Verwendung
ganz rudimentärer Mittel ist möglich. So verwendet zum Beispiel Rick Sternbach, Senior
Illustrator und Technical Consultant von Star Trek: Voyager, kein hochkompliziertes
3D-Vektorzeichenprogramm o.ä. zum Berechnen des Kurses der Voyager, sondern zeichnet die
Routenpunkte auf ganz gewöhnliches 11'x17' Millimeterpapier. Manchmal ist es in der Tat
nützlich (vor allem bei Karten), sich etwas auf einem Stück Papier direkt vor Augen zu
führen, doch soll in diesem Projekt so oft wie möglich auf die genauesten Methoden
zurückgegriffen werden, also auf mathematische Berechnungen und elektronische Bild- und
Datenverarbeitung.
Zu den weiteren
Voraussetzungen gehört damit natürlich auch eine genaue Kenntnis der Datenbasis, die
ausgewertet werden soll. Im Fall der Star Trek Kartographie ist dies die Kenntnis aller
Star Trek Episoden, Filme und Bücher. Dies ist jedoch nur ein Teil der speziellen
Anforderungen der Star Trek Kartographie. In der Tat spielt die Astronomie eine
außerordentlich große Rolle, die nicht unterschätzt werden sollte. Letztendlich geht es
in diesem Projekt nur um Astronomie, und wenn auch die Datenbasis fiktiv sein mag, so sind
zu deren Verwendung neben den kartographischen vor allem astronomische Methoden
notwendig. Neben astronomischem Material (Himmelskarten, astronomische Datentabellen usw.)
schließt dies auch dreidimensionale Raumgeometrie und astronomische Berechnungen ein.
Eine Gesamtdarstellung des für dieses Projekt notwendigen Materials - sowohl in Bezug auf
Star Trek als auch die Astronomie - finden Sie in den Quellen.
Aber auch das Projekt selbst bietet verschiedene, speziell auf für Star Trek Kartographie
erstellte Tabellen und Datenzusammenstellungen, die für die weitere Arbeit nützlich
sind. Sie sind im Bereich "Ressourcen" zusammengefaßt, während sie spezielle
Algorithmen der Star Trek Kartographie als "Interaktive Programme"
enthalten sind.
Nach dieser allgemeinen Darstellung der notwendigen Mittel und Methoden sollen im
folgenden nun die wichtigsten Aspekte der Star Trek Kartographie etwas genauer beleuchtet
werden.
1.2.2 Entfernungen als Basis für die Kartographie
Da uns bei Star Trek leider in den seltensten Fällen bereits fertige Karten zur Verfügung stehen und wenn, dann nur für einen von der Mission erforderten, winzigen Teil des Weltraums, aber nie vom gesamten erforschten Raum, muß meistens auf die kleinsten Bausteine der Star Trek Kartographie zurückgegriffen werden, mit denen das fertige Bild des Universums erst aufgebaut werden muß: die in den Episoden, Filmen und Büchern gegebenen Entfernungen. Haben wir eine genügend große Anzahl von Entfernungen gegegen, die in einem wechselseitigen Zusammenhang stehen (d.h. für jeden Ort muß eine Entfernung zu jedem anderen Ort bekannt sein), so läßt sich auf Basis dieser Entfernungen eine Karte erstellen. Jedoch ist die Sache nicht ganz so einfach, da wir niemals diesen kompletten Satz von Entfernungen zur Verfügung haben und unser Wissen, bedingt durch die untergeordnete Rolle, die die Kartographie in Star Trek hat, immer lückenhaft ist. Mit einem solchen offenen Netz an Entfernungsangaben sind eindeutige Karten auf jeden Fall ausgeschlossen, so daß wir uns nur - wie schon in der Einführung erwähnt - auf Vermutungen, Spekulationen und logische Annahmen, der wohl zweitwichtigste Grundpfeiler der Star Trek Kartographie, stützen können und es akzeptieren müssen, das ein eindeutiges, nicht interpretationsfähiges Bild des Star Trek Universums niemals geben wird, auch wenn eines Tages z.B. ein offizielles technisches Handbuch eine der Möglichkeiten offiziell macht.
Die Verwendung von Entfernungen als Basis für die kartographische Arbeit wird noch dahingehend schwieriger gemacht, daß wir in den seltensten Fällen direkte Angaben zur Verfügung haben. Insgesamt können auf 4 verschiedene Arten Entfernungen aus den offiziellen Quellen (Episoden, Filme, Bücher, elektronische Medien) ermittelt werden, die im folgenden näher beleuchtet werden.
 |
Eine fast vollständige Zusammenstellung aller in den Serien, Filmen und Büchern direkt gegebenen sowie der auf Basis der vorgestellten Methoden ermittelten Entfernungen finden Sie in der Übersicht Star Trek Entfernungen. |
1. Direkte Entfernungsangaben
Allgemein gehen die Episoden und Kinofilme sehr sparsam mit der Angabe von Entfernungen im Dialog oder auf Computerdisplays u.ä. um, allenfalls bei Star Trek: Voyager findet man häufiger Angaben zur Entfernung von in der Nähe der Route der USS Voyager gelegenen Objekten. Trotzdem gibt es für die Entfernungen zwischen fast allen wichtigen Planeten (d.h. den Hauptplaneten der Bündnisse und Imperien) Angaben, was wir neben einigen Schlüsselepisoden auch offiziellen Dokumentationen wie dem ST:DS9 Technical Manual zu verdanken haben. Sind in solchen Büchern Entfernungen aufgelistet bzw. werden in Dialogen Entfernungen genannt, so liegen sie meistens in der populärwissenschaftlichen Einheit Lichtjahr (ly) vor, in Einzelfällen wurden jedoch auch schon die Einheiten Astronomische Einheit (AE) und Parsec (pc) verwendet. Obwohl die direkte Entfernungsangabe die schnellste und bequemste Weise ist, um an Informationen zu Sternpositionen und -entfernungen zu kommen, ist in diesen Fällen bereits eine mathematische Umrechnung nötig, da natürlich alle Entfernungen zur Auswertung und Kombination in Karten in jeweils derselben Einheit (in der Astronomie das Parsec, bei Star Trek und damit in diesem Projekt bevorzugt das Lichtjahr) vorliegen müssen.
| Einheit | Definition | Umrechnung |
| Lichtjahr (ly) | Die Strecke, die das Licht im Vakuum (V=299792 km/s) in einem Jahr zurücklegt. | 1 ly = 9.461x1012
km 1 ly = 6.323x104 AE 1 ly = 0.307 pc |
| Parsec (pc) | Die Entfernung, aus der eine astronomische Einheit unter einem Winkel von einer Bogensekunde sichtbar wird. | 1 pc = 3.086x1013
km 1 pc = 2.063x105 AE 1 pc = 3.262 ly |
| Astronomische Einheit (AE) | Mittlerer Abstand der Erde von der Sonne. | 1 AE = 149.6x106 km 1 AE = 1.582x10-5 ly 1 AE = 4.847x10-6 pc |
2. Entfernungen über Zeit und Geschwindigkeit ermitteln
Vor allem bei Star
Trek: The Next Generation, aber auch vereinzelt in den anderen Serien und den Filmen
findet man eine wichtige indirekte Form der Entfernungsangabe, die eng an das
interstellare Reisen mit einem Raumschiff gekoppelt ist: die Nennung von Warpfaktor und
Zeit. Ein typisches Beispiel ist, daß wir den gegenwärtigen Standort eines Raumschiffes
wie der USS Enterprise-D kennen und wir im Dialog, bei The Next Generation bevorzugt mit
Lt. Cmd. Data, die nötige Warpgeschwindigkeit mitgeteilt bekommen, bei der das Schiff in
einer bestimmten Zeit sein Ziel erreicht. Unbedingte Voraussetzung ist bei dieser Methode
also neben Zeit und Geschwindigkeit die Kenntnis des Start- und Zielpunktes, da sonst die
Angabe nutzlos ist.
Sind alle Größen gegeben, so ist die Entfernungsbestimmung ziemlich einfach, da nun nur
noch mathematischen Standardformeln (s=V*t) die Entfernung bestimmt werden muß. Hierbei
muß aber beachtet werden, daß wir bei Star Trek die Geschwindigkeit niemals in km/s
vorliegen haben, sondern in Warp bzw. Impuls vorliegen haben und damit das Problem
besteht, wie man diese speziellen Entfernungsmaße in SI-Einheiten umrechnet.
Glücklicherweise gibt das ST:TNG Technical Manual und die Star Trek Enzyklopädie genaue
Auskunft über den Faktor der Lichtgeschwindigkeit (c) bzw. km/s, die bestimmten
Warpfaktoren oder Impulsanteilen entsprechen, so daß in den meisten Fällen die
Berechnung kein Problem sein sollte.
| Geschwindigkeit | c | km/s |
| 1/4 Impuls | 0.0625 | 18737 |
| 1/2 Impuls | 0.125 | 37474 |
| Voller Impuls | 0.25 | 74948 |
| Warp 1 | 1 | 299792 |
| Warp 2 | 10 | 2997920 |
| Warp 3 | 39 | 11691888 |
| Warp 4 | 102 | 11691888 |
| Warp 5 | 214 | 30578784 |
| Warp 6 | 392 | 64155488 |
| Warp 7 | 656 | 117518464 |
| Warp 8 | 1024 | 306987008 |
| Warp 9 | 1516 | 454484672 |
| Warp 9.2 | 1649 | 494357008 |
| Warp 9.6 | 1909 | 572302928 |
| Warp 9.9 | 3053 | 915264976 |
| Warp 9.99 | 7912 | 2371954304 |
| Warp 9.9999 (Subraumfunk) | 199516 | 59813300672 |
Leider ist es aber nicht immer ganz so einfach, daß man einfach nur einen Wert aus einer
Tabelle ablesen braucht. Teilweise ist die Geschwindigkeit nämlich nicht direkt gegeben,
sondern wird nur mit Phrasen wie "bei sehr hoher Warpgeschwindigkeit" oder
"bei Maximum Warp" umschrieben. Bei unbestimmten Ausdrücken ist es generell nur
möglich, einen Geschwindigkeitsbereich und damit auch nur einen Entfernungsbereich
(Minimal- und Maximalentfernung) anzugeben, jedoch gibt es eine Möglichkeit zur genauen
Bestimmung, wenn von "Maximum Warp" die Rede ist. Es sind nämlich von recht
vielen Schiffsklassen die Maximalgeschwindigkeiten genau bekannt, wobei aber - abhängig
von der Zeitangabe - unbedingt zwischen Höchstgeschwindigkeit (für jede beliebige Zeit)
und Maximalgeschwindigkeit (nur bis zu einer bestimmten Zeit; meistens 12h) unterschieden
werden muß. Ein weiteres Problem ist, daß die neueren Klassen wie Defiant-, Sovereign-
und Intrepid Klasse Maximalgeschwindigkeiten haben, die in keiner offiziellen Tabelle
stehen. Hier können dann nur semi-offizielle Näherungsgrößen verwendet werden, die Sie
unter folgender Tabelle zusammengestellt finden.
| Klasse | Höchstgeschwindigkeit | Maximalgeschwindigkeit (12h) |
| Miranda Klasse | Warp 9.2 | |
| Nebula Klasse | Warp 9.6 | |
| Galaxy Klasse | Warp 9.2 | Warp 9.6 |
| Akira Klasse | Warp 9.8 | |
| Defiant Klasse | Warp 9 | Warp 9.982 |
| Intrepid Klasse | Warp 9.975 | |
| Sovereign Klasse | Warp 9.95 |
| Geschwindigkeit | c | km/s |
| Warp 9.8 | ~2500 | 749480000 |
| Warp 9.95 | ~5500 | 1648856000 |
| Warp 9.975 | ~6667 | 1998713264 |
| Warp 9.982 | ~7500 | 2248440000 |
Richtig schwierig wird es jedoch, wenn ein gebrochener Warpfaktor gegeben ist, der in
keiner der obenstehenden Tabellen erwähnt wird. Dann sind wir auf eine Umrechnungsformel
von Warp zu c angewiesen, die leider in keiner offiziellen Dokumentation zu finden ist.
Der einzige Anhaltspunkt ist der genaue Graph des Verlaufs der sog. Warpfunktion, bei der
sich der Faktor der Lichtgeschwindigkeit gegen unendlich strebt, wenn der Warpfaktor gegen
10 gibt (asymptotischer Verlauf). Zahlreiche populäre, von Fans entwickelte Formeln
basieren auf diesem Graphen, jedoch kann keine den Verlauf 100% genau nachbilden. Dies ist
nur bis Warp 9 möglich, denn bis dahin hat die Funktion einen recht einfachen Verlauf:
f(x)=x(10/3)
Erst zwischen Warp 9 und 10 wird die asymptotische Steigerung wirksam, so daß ein Korrekturglied eingefügt werden muß. Eine mögliche Formel dafür ist
f(x)=x
(10/3)+(10-x)(-11/3)die jedoch nur bis Warp 9.6 die exakten, in der Tabelle zu findenden Faktoren der Lichtgeschwindigkeit wiedergibt.
 |
Die automatische Berechnung von Entfernungen auf Grundlage der Zeit und von ganzen oder gebrochenen Warpfaktoren bis Warp 9.6 ist mit dem interaktiven Programm Warp-Zeit-Strecke möglich |
3. Entfernungen von realen Sternen
Das es sich bei dem
Ziel gerade um einen "echten" Stern handelt, ist natürlich recht
unwahrscheinlich, doch es ist schon ziemlich oft vorgekommen, vor allem in der
klassischen Star Trek Serie. Insgesamt wurden bei Star Trek 34 Sterne im Dialog
erwähnt bzw. waren teilweise sogar als Ort Bestandteil der Handlung.
Ist die Möglichkeit tatsächlich gegeben, brauchen wir dann nur noch den Stern in einem
Sternenatlas nachschlagen und finden hoffentlich eine Entfernungsangabe vor. Eine gewisse
Unsicherheit bleibt aber, da leider aufgrund unterschiedlicher bzw. ungenauer
Bestimmungsmethoden häufig immer immer noch keine Einigkeit über die exakte Entfernung
einiger Sterne besteht.
| Vor allem die am häufigsten eingesetzte Entfernungsbestimmung über die Sternenparallaxe (der Winkel, unter dem man von diesem Stern den Halbmesser der Erdbahn, d.h. den Abstand Erde-Sonne sehen würde) wird mit größer werdender Entfernung des Sterns immer ungenauer, bis die Fehlerabweichung die eigentlichen Entfernung übersteigt und die Messung somit nutzlos ist. Das große Problem hierbei ist, das bei der Parallaxenbestimmung mit herkömmlichen, erdgebundenen Teleskope große Fehlerabweichungen schon bei geringen Entfernungen auftreten, da sie Winkel nur auf einige tausendstel Bogensekunden (") genau messen können: bei 30 ly 7%, bei 150 ly 35% und bei 350 ly sogar 70%. | 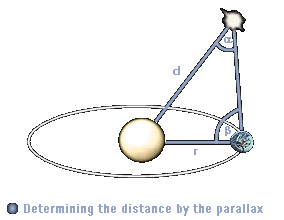 |
Daß uns trotzdem für alle 35 Sterne um vieles genauere Entfernungen zur Verfügung stehen, haben wir ausschließlich der HIPPARCOS Mission zu verdanken, bei der von 1989 bis 1993 ein Satellit fern von den störenden Einflüssen der Erdatmosphärt die Entfernung zu den wichtigsten Sternen mit nie dagewesener Präzision gemessen hat. Seit 1997 steht der HIPPARCOS Katalog zur Verfügung, aus dem die Entfernungen aller in diesem Projekt aufgelisteten realen Sterne stammen.
 |
Eine Übersicht über die bei Star Trek erwähnten realen Sterne, ihre Parallaxen und Entfernungen finden Sie in der Tabelle Die Positionen der realen Sterne. |
4. Entfernungen in Karten
nachmessen
Es kommt ziemlich
selten vor, daß bei Star Trek onscreen Karten von bestimmten Gebieten der Galaxis zu
sehen sind, und so gut wie nie, daß wir eine Gesamtkarte zu Gesicht bekommen. Häufig
besteht auch das Problem, daß die Karten - meistens auf Computerbildschirmen zu sehen -
viel zu klein, undeutlich und verschwommen sind, als daß sie von praktischen Nutzen
wären. Nichtsdestotrotz gibt es doch eine beachtliche Anzahl an uns bekannten Karten aus
Star Trek: Voyager, Star Trek: Deep Space Nine sowie aus offiziellen Dokumentationen wie
dem ST:DS9, die wir für die kartographische Auswertung verwenden können. Das eigentliche
Nachmessen von Entfernungen gestaltet sich recht problemlos, jedoch gibt es gewisse
Einschränkungen und Hürden, die vorher erst zu nehmen sind.
Grundsätzlich können wir nur Entfernungen nachmessen, wenn wir das Pixel-Lichtjahre-Verhältnis der Karte kennen. Diesen können wir aus dem
Maßstab der Karte berechnen. Damit scheidet bereits ein Großteil der uns zur Verfügung
stehenden Karten aus, denn die wenigsten geben einen Maßstab an. Bisher ist dies nur bei
den im ST:DS9 TM enthaltenen Karten der Fall. Hier haben wir ausdrücklich in den Karten
einen Meßbalken enthalten, mit dessen Hilfe wir die gewünschte Entfernung recht einfach
berechnen können. Mit dem Lineal und einem Taschenrechner geht das sicher am schnellsten,
doch für wirklich 100% genaue Ergebnisse sollte die gewünschte Karte möglichst
verzerrungsfrei eingescannt und dann mit einem Bildbearbeitungsprogramm die
einzelnen Abstände nachgemessen werden. Am einfachsten ist dies in einem Programm, daß
die Länge von Linien angeben kann, doch leider haben diese nützliche Funktion die
meisten Bildbearbeitungsprogramme nicht. Also benötigen sie noch einen Taschenrechner, um
über rechtwinklige Dreiecke die Abstände berechnen zu können. Im folgenden ein
einfaches Beispiel:
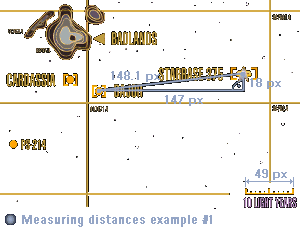
| 1. Zuerst muß das
Pixel-Lichtjahre-Verhältnis bestimmt werden. Messen Sie dazu die Länge des Meßbalkens
und berechnen sie das Verhältnis: Verhältnis=Lichtjahre / Länge = 10 ly / 49 px = 0.204 ly/px 2. Messen Sie entweder die Länge der Verbindungslinie zwischen den Start- und Zielpunkt direkt oder konstruieren Sie ein rechtwinkliges Dreieck, dessen Ankatheten- und Gegenkathetenlänge Sie messen und dann mit dem Satz von Pythagoras die Hypothenusenlänge berechnen. Pixellänge=sqr(a²+b²)=sqr((147 px)² * (18 px))²=148.1 px 3. Multiplizieren Sie Pixellänge mit dem Pixel-Lichtjahre- Verhältnis der Karte, um die gesuchte Entfernung zu erhalten. Entfernung=148.1 px * 0.204 ly/px = 32.22 ly |
 |
Enthalten die Karten keinerlei Maßstabsangabe, gibt es trotzdem manchmal noch eine
Chance, das Pixel-Lichtjahre-Verhältnis herauszubekommen, nämlich immer dann, wenn
Strecken in der Karte enthalten sind, deren Länge bereits bekannt ist. Das Verhältnis
wird dann durch Nachmessen der Linienlänge bzw. Konstruieren eines rechtwinkligen
Dreiecks und Verwendung des Satzes von Pythagoras bestimmt und kann wie in der obigen
Rechnung dann für die Umrechnung der Pixellänge in die gesuchte Entfernung verwendet
werden, wie folgendes zweites Beispiel zeigt.
| 1. In der
nebenstehenden Karte ist keinerlei Maßstab gegeben; jedoch ist uns der Durchmesser der
Romulanischen Neutralen Zone aus The Next Generation bekannt: 1 ly. Über den Satz von
Pythagoras haben wir auf der Karte für den Durchmesser eine Länge von 25.5 px erhalten,
womit wir das Verhältnis berechnen können: Verhältnis=Lichtjahre / Länge = 1 ly / 25.5 px = 0.039 ly/px 2. Diesmal soll der Abstand von Romulus zur neutralen Zone bestimmt werden. Hierbei ist zu beachten, daß sich der Punkt-Gerade-Abstand immer dem Lot durch den Punkt auf die Gerade bezieht, d.h. die Verbindungsgerade muß senkrecht auf der Grenzlinie der RNZ stehen, damit wir wirklich den kleinsten Abstand erhalten. Da es sich wieder um eine schräge Linie handelt, verwenden Sie den Satz von Pythagoras, um den Abstand zu erhalten: Pixellänge=sqr(a²+b²)=sqr((76 px)² * (28 px))²=81 px 3. Multiplizieren Sie nun Pixellänge mit dem Pixel-Lichtjahre- Verhältnis der Karte, um den Abstand von Romulus zur Neutralen Zone zu erhalten. Entfernung=81 px * 0.039 ly/px = 3.18 ly |
|
Ein letzter Hinweis für das Nachmessen von Entfernungen in Karten: Karten der realen
Galaxis sind für das Messen nur bedingt geeignet, da diese natürlich
eine zweidimensionale Umsetzung der realen Positionen der Sterne im dreidimensionalen
Raum sind. Somit geben die abzulesenden Entfernungen immer nur einen Mindestabstand zur
Erde an, und die Wahrscheinlichkeit ist groß, daß der jeweilige Stern sehr viel weiter
entfernt ist, weil sich die meisten nicht in der gleichen Ebene wie die Erde befinden.
Dreidimensionale Karten dagegen können ohne erheblichen Rechenaufwand überhaupt nicht
für die Entfernungsbestimmung herangezogen werden.
 |
Zahlreiche Karten sowohl aus echten Astronomiebüchern als auch aus Star Trek Episoden und Dokumentationen, aus denen Sie Entfernungen entnehmen können, finden Sie im Karten-Archiv. |
1.2.3 Der Nutzen von realen Sternen für die Kartographie
Neben den Entfernungen
und Planeten in bereits vorhandenenen offiziellen Karten ist es möglich, noch weitere
Fixpunkte aus den Episoden, Filmen und offiziellen Dokumentationen zu ermitteln, in dem
wir die 34 realen Sterne bei Star Trek betrachten. Dies haben wir bereits im letzten
Abschnitt zur Entfernungsbestimmung zwischen Stern und Erde getan, um aus dem komplexen
Geflecht von Entfernungen Rückschlüsse auf die räumliche Situation zu ziehen.
Nun wollen wir einen Schritt weiter gehen und die wirklichen Positionen der
realen Sterne im dreidimensionalen Raum bestimmen. Das ist natürlich mit einem enormen
Aufwand verbunden, aber uns auch einen bedeutenden Schritt näher zu einer gleichzeitig
realistischen und eng an die Episoden angelehnten Karte bringen wird, weil wir genügend
reale Sterne kennen, um sie als "Grundgerüst" für alle fiktiven Elemente der
Karte zu benutzen.
Um die realen, also
erdunabhänigen Positionen von Sternen in der Galaxis bestimmen zu können, ist es
zwangsläufig nötig, sich etwas näher mit dem galaktischen Koordinatensystem zu
beschäftigen, ein sehr mächtiges, aber von den Astronomen recht vernachlässigtes
astronomisches System.
Das galaktische Koordinatensystem wurde aus der Notwendigkeit heraus entwickelt, daß man,
mit fortschreitender Erforschung unserer Galaxis und ihrer Struktur, mehr über die
Konzentration und Verteilung der Sternen in der Milchstraße erfahren wollte. Dieser
Stellarstatistik genannte Teilbereich der Astronomie ist jedoch mit den gebräuchlichen
Koordinatensystemen (z.B. das Äquatorialsystem) nur äußerst umständlich zu
bewerkstelligen, da zur Ermittlung der tatsächlichen Anordnung der Sterne im Raum und
nicht nur der am Himmel zusätzlich zur Rektaszension und Deklination immer auch eine
Entfernung benötigt wird. In den galaktischen, auf die Milchstraße bezogenen Koordinaten
dagegen sind zur Feststellung der Sternverteilung keinerlei zusätzliche
Entfernungsangaben notwendig.
Das galaktische Koordinatensystem geht nämlich als einziges nicht von erdgebundenen (und
teilweise auch zeit- und ortsabhängigen) Himmelskoordinaten aus, sondern nutzt Punkte in
übergeordneten Systemen als Definitionsparameter. Als Bezugsebene oder Grundkreis dieses
Koordinatensystems dient die galaktische
Ebene (die Symmetrieebene der
Galaxis), als Bezugspunkt nimmt man das galaktische Zentrum. Dieses ist zugleich der Nullpunkt der Längenzählung, d.h., die
Richtung zum galaktischen Zentrum hat eine galaktische Länge von 0°. Die galaktische Länge l ist das Pendant zur Rektaszension (dem
Azimutalwinkel) im Äquatorialsystem und steigt in gleicher Richtung (also gegen den
Uhrzeigersinn) in einem Gradsystem von 0° bis 360° an. Die zweite notwendige Koordinate
ist das Pendant zur Deklination (dem Höhenwinkel), die galaktische Breite b, die vom galaktischen Nordpol mit b=90° über die galaktische Ebene mit
b=0° zum galaktischen Südpol mit b=-90° abfällt.
Um nun also beide galaktischen Koordinaten aus den äquatorialen berechnen können, werden
zumindest die Koordinaten von zwei Fixpunkten benötigt: das galaktische Zentrum und der
galaktische Nordpol. Beide Größen stehen derzeit nur für das Äquinoktium (die
astronomische Epoche) 1950.00 zur Verfügung. Das galaktische Zentrum hat dabei die
Rektaszension 17h42.4min und die Deklination -28°.92 und der
galaktische Nordpol hat die Rektaszension 12h49min und die
Deklination +27°.4.
Im folgendenen soll nun am Beispiel Vulcan (=o2 Eridani bzw. 40 Eridani)
gezeigt werden, wie galaktische Koordinaten berechnet werden können:
1. Wir suchen die Äquatorialkoordinaten des Sterns. Vulcan hat die Rektaszension 04h13min und die Deklination -7°.44'.
2. Für die Rektaszension ist eine Umrechnung von Zeitmaß (Stunden h, Zeitminuten min und Zeitsekunden s) in das von der Deklination und auch den galaktischen Koordinaten verwendete Gradmaß (Grad °, Bogenminuten ' und Bogensekunden '') nötig. Dazu dividieren wir die Zeitsekunden (wenn vorhanden) durch 60, addieren dazu die Zeitminuten, teilen das Ergebnis wiederum durch 60 und addieren die Stunden, um eine Rektaszension nur in Stunden (als Dezimalzahl) zu erhalten. Für Vulcan ist das (13/60)+04=4.h21667. Um den Winkel in Zeitmaß in Winkelgrade umzuwandeln, muß dieses Ergebnis nun mit 15 (1h=15°) multipliziert werden: 4.h21667*15=63°.25.
3. Zur eigentlichen Umrechnung in galaktische Koordinaten werden Gleichungen der sphärischen Trigonometrie benötigt. Die galaktische Breite b berechnen wir aus der Rektaszension a und der Deklination d mit
sin b=sin d * cos 62°.6 - cos d * sin 62°.6 * sin(a-282°.25)
Für Vulcan erhält man dann sin b=-0.6136 und damit b=-37°.85.
Für die etwas kompliziertere Berechnung der galaktischen Länge d benötigen wir die soeben berechnete galaktische Breite:
cos(l-33°) = ( cos d * cos(a - 282°.25) ) / (cos b)
Für Vulcan erhalten
wir sin l-33°=-0.9759 und damit l-33°=167.4° und schließlich l=200.4°.
Das Problem bei diesen in Fachwerken angegeben Formeln ist, das sie merkwürdigerweise nicht immer richtige Werte liefern. So stimmt die berechnete galaktische Breite zwar immer, aber die galaktische Länge weicht bei etwa der Hälfte der Werte um 0° bis 200° ab. Das ist natürlich inakzeptabel, so daß eine zweite Methode zur Ermittlung der galaktischen Koordinaten nötig ist, um Vergleichswerte zu den berechneten zu erhalten. Diese zweite Methode verwendet bereits von Sternwarten vorgefertigte Diagramme, die die äquatorialen und galaktischen Koordinaten graphisch in Beziehung setzen und sich
Was können wir nun
mit diesen galaktischen Koordinaten anfangen? Wenn man die Fixpunkte des galaktischen
Koordinatensystems anschaut - Nordpol, Südpol, galaktische Ebene (also Äquator), wird
klar, daß die Sterne in diesem System quasi an eine galaktische Sphäre projiziert, deren Äquator die galaktische
Ebene ist. Wir können nun die Erde in den Mittelpunkt der galaktischen Sphäre setzen, da
diese sehr nah bei der galaktischen Ebene liegt und wir somit alle Definitionsparameter
(galaktischer Nordpol, Nullrichtung) durch unser erdbezogenes Äquatorialsystem festgelegt
haben.
Zeichnen wir in ein Modell des galaktischen Koordinatensystems die Fixpunkte, die Erde und
einen Stern, dessen Position festgestellt werden soll, ein, wird ersichtlich, daß sich
mit einfachen trigonometrischen Berechnungen die Position des Sterns relativ zur Erde
ermitteln läßt.
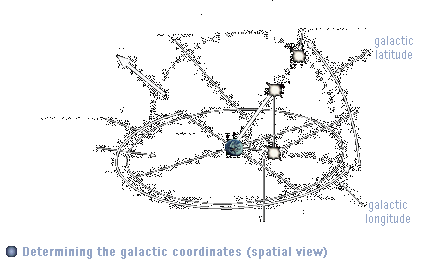
| Dazu benötigen wir
erstens Höhen- und Azimutalwinkel, die wir in Form der galaktischen Koordinaten bereits
gegeben haben, sowie den Abstand des Sterns auf der galaktischen Ebene. Letzteren können
wir durch die Winkelbeziehung von der realen Entfernung des Sterns (die die Hypothenuse
eines rechtwinkligen Dreiecks bildet) und der galaktischen Breite (dem eingeschlossenen
Winkel) ermitteln: dEbene=cos(b) * d Mit Ebenenabstand und den 2 Winkeln lassen sich nun X, Y und Z Abstand des Sterns von der Erde recht einfach ermitteln, in dem wir die Länge der Linien mit dem Startpunkt (0,0,0), also der Erde, der Länge dEbene und dem Winkel l oder b berechnen:
Yrelativ=.-cos(lBogen) * dEbene bBogen=b*(pi/180°) |
|
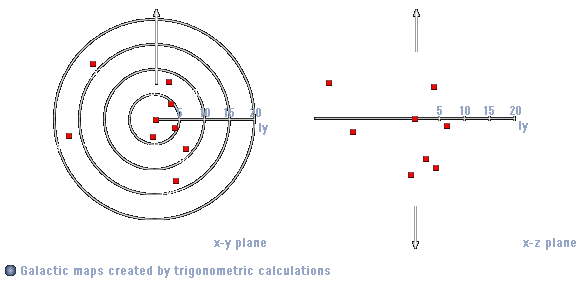
Betrachten wir die galaktische Ebene "von oben", so gedreht, daß 0° galaktische Länge genau die vertikale Schnittgerade des galaktischen Äquators darstellt, so liegen alle Sterne mit positiver relativer X-Koordinate rechts von der Erde auf der Ebene, mit positiver relativer Y-Koordinate unter der Erde auf der Ebene, und mit positiver Z-Koordinate oberhalb der galaktischen Ebene. Der Stern im obigen Beispiel hat somit positive X, Y und Z Koordinaten.
Wiederholt man die beschriebene Prozedur für eine genügend große Anzahl von Sternen und transformiert man die relativen Koordinaten entsprechend eines festgelegten Pixel/Lichtjahre Verhältnisses, können ohne Probleme galaktische Karten erstellt werden.
 |
Eine komplette Auflistung aller 34 bisher bei Star Trek erwähnten echten Sterne und ihrer Entfernungen, galaktischen Koordinaten und daraus berechneten absoluten Koordinaten in verschiedenen System finden Sie in der Tabelle Die Positionen der realen Sterne. |
Nun, da Sie mit dem Grundlagenwissen der Star Trek Kartographie und vertraut sind und erfahren haben, wie die einzelnen Hilfsmittel und Methoden angewendet werden, kann die eigentliche Reise durch die Star Trek Galaxis beginnen.
© 1999-2001 by Star Trek Dimension / Webmaster. Letzte Änderung: 14.02.2000